1.题目
DF-ResNet: Boosting Speaker Verification Performance with Depth-First Design
2.总结
在作者发现这一重要结论 (depth is more important than the width of networks for speaker verification task) 后,作者提出了一种新的但是却又完全基于标准的卷积网络的结构。该结构的设计基于深度优先的规则,虽然在提升网络的层数,但能保持复杂度不会大幅度上升,在此基础上取得了很好的效果。作者将其应用到了ResNet上构造出了DF-ResNet,并与ECAPA和ResNet做了比较,如下图。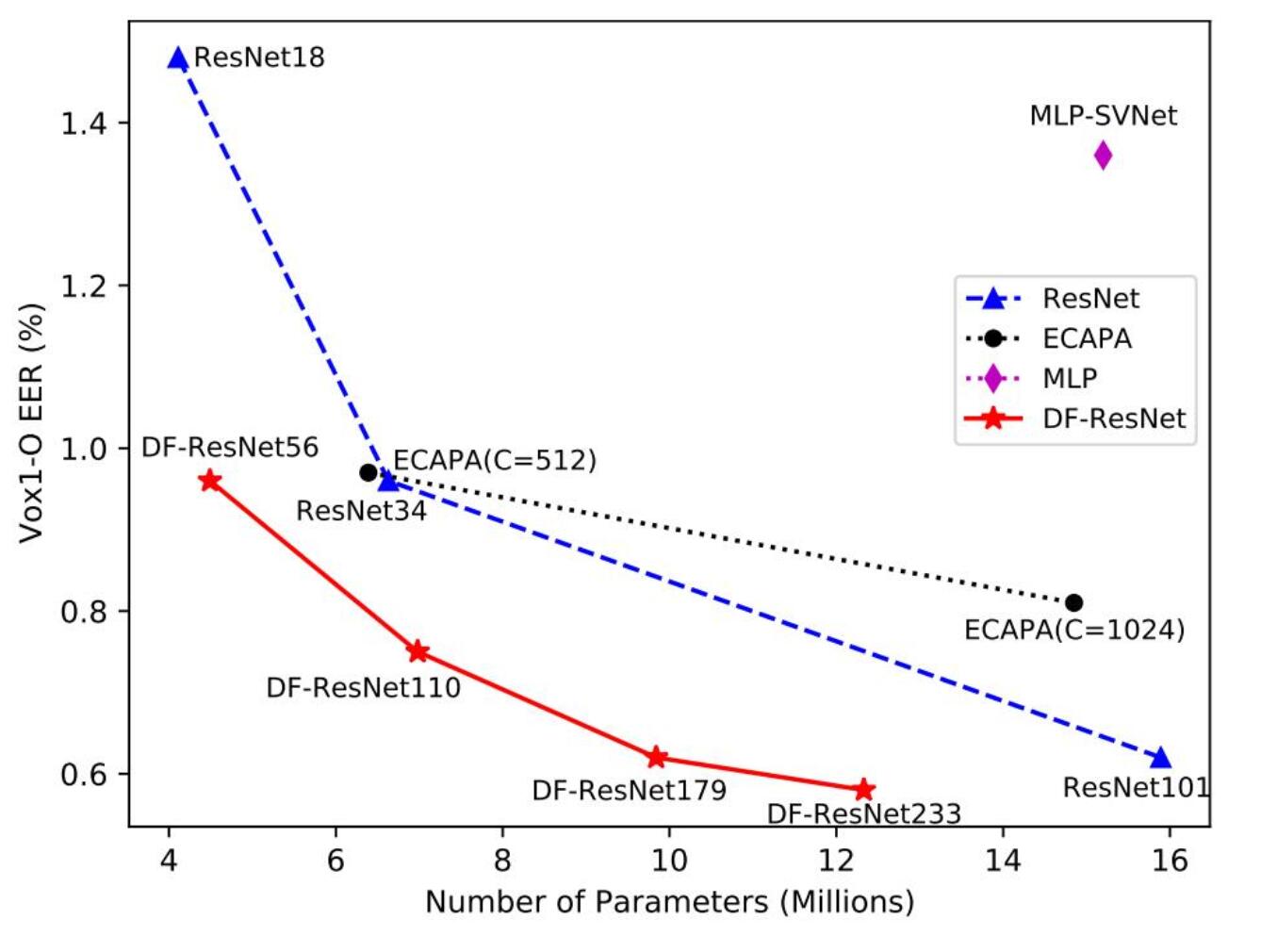
3.研究目标
作者通过研究发现对于说话人识别任务来说,深度相较于宽度对于网络来说是更加重要的。于是作者为了验证这个说法开始了一系列验证。
4.使用方法
作者提出了基于深度优先的规则来深化网络,下图展示了从ResNet18到DF-ResNet56的转换过程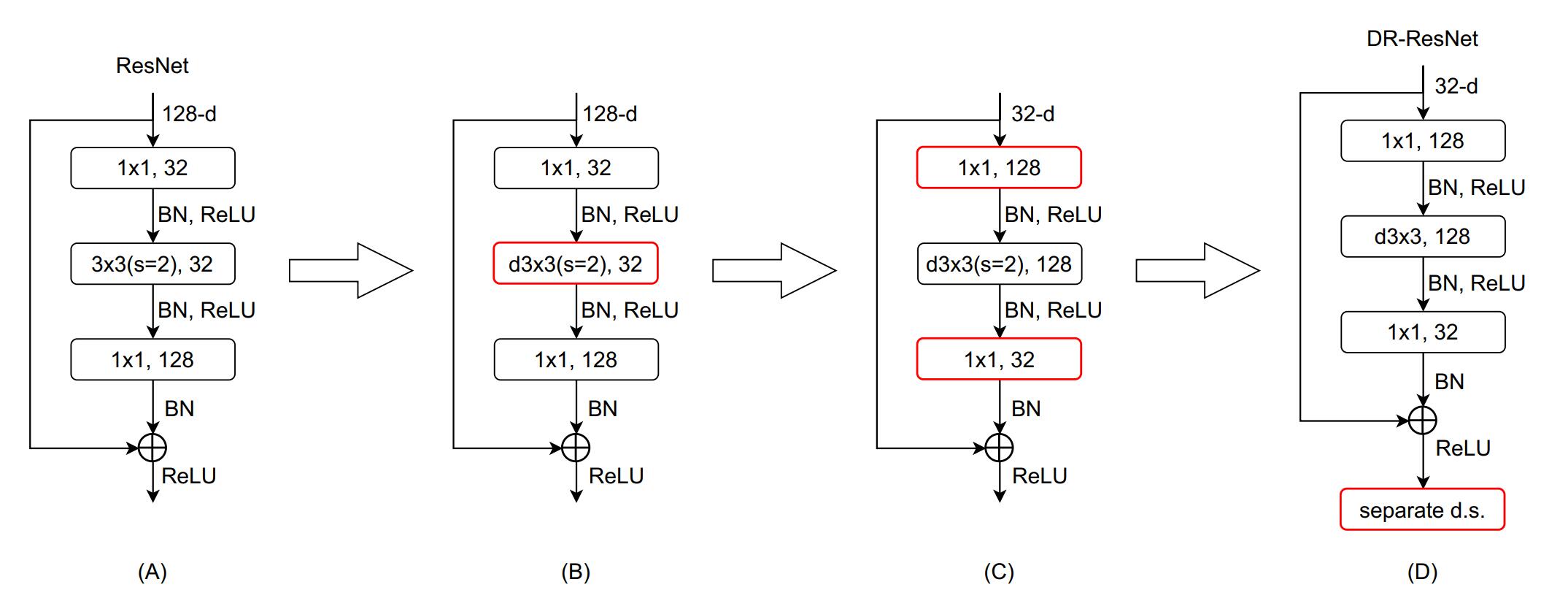
- A图:原生ResNet的瓶颈模块
- B图:用depthwise convolution来代替标准的卷积
- C图:交换两个1×1卷积的位置,并将depthwise convolution的通道数增加到128
- D图:加入一个单独的下采样层
深度优化设计规则:需要注意的是这并不是直接增加层数的数量,关键要义是神话网络的同时还要保证模型复杂度不能变化太大。
下表为从ResNet18到DF-ResNet56各个过程中参数数量、FLOPs和模型效果数值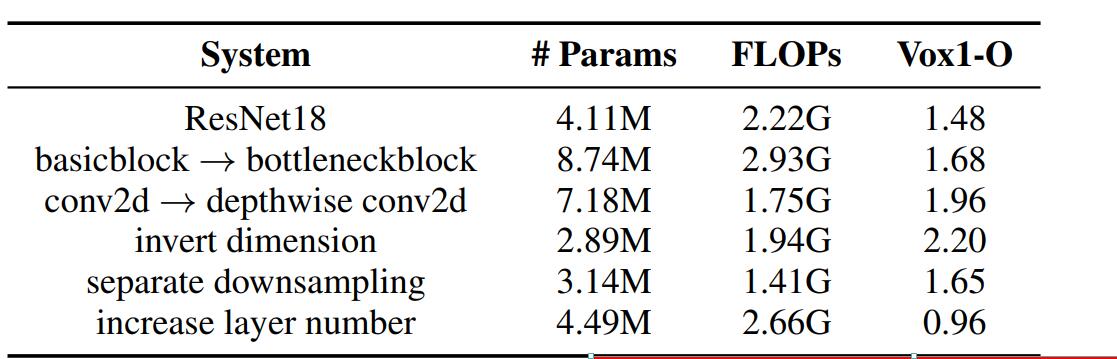
- basicblock → bottleneckblock
在将ResNet18中的基本模块更换之后发现效果反而变差,所以可以看出这种瓶颈层对ResNet影响不大,这就有必要去重新设计它。
- conv2d → depthwise conv2d
采用depthwise conv2d去代替普通的卷积(depthwise conv2采用一种特殊的组数等于通道数的组卷积)
- invert dimension
这里将瓶颈层倒置,瓶颈层一般是为了加深深度减少参数量和计算量提出的一种结构,按理说倒置后会出现相反的结果。但是在这里参数量骤减、计算量降低了一点点,效果却只是差了一丢丢而已。这是因为除了倒置,还将中间第二层的卷积分为了128组,这才导致了参数量和计算量的减少。
- separate downsampling
将一个单独的降采样层放在模块的最后进一步提取特征。
- increase layer number
在利用depthwise conv2d减少参数量和计算量后,再不断加入层数优化网络。
5.结论
其实就是作者不断在文章中提到的这句话:
depth is more important than the width of networks for speaker verification task.
6.额外笔记
6.1 depthwise conv2d
depthwise conv2d是一种特殊的分组卷积,那么什么又是分组卷积呢?其实最早在读AlexNet时,因为当时硬件资源有限,训练时卷积无法放到一个GPU里。于是作者将特征一分为二,放在两个GPU里分别进行卷积,直到最后处理完毕才将两份特征进行融合。
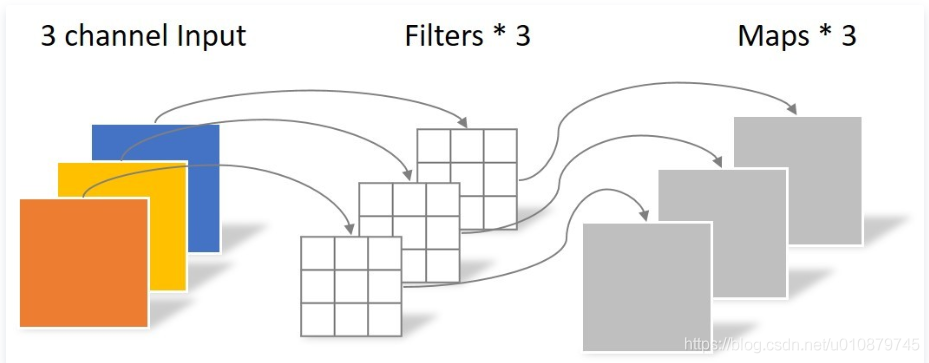
现如今我们的硬件资源已经得到了很大的提升,那么是否这种分组卷积的方法就没有必要再使用了呢?答案是否定的。下面我们来分析一下。(示意图不是很好,因为输出通道都是1,搞得我理解的时候刚开始出现了好大的偏差,以下图中未出现的C’均为输出通道)
- 标准卷积
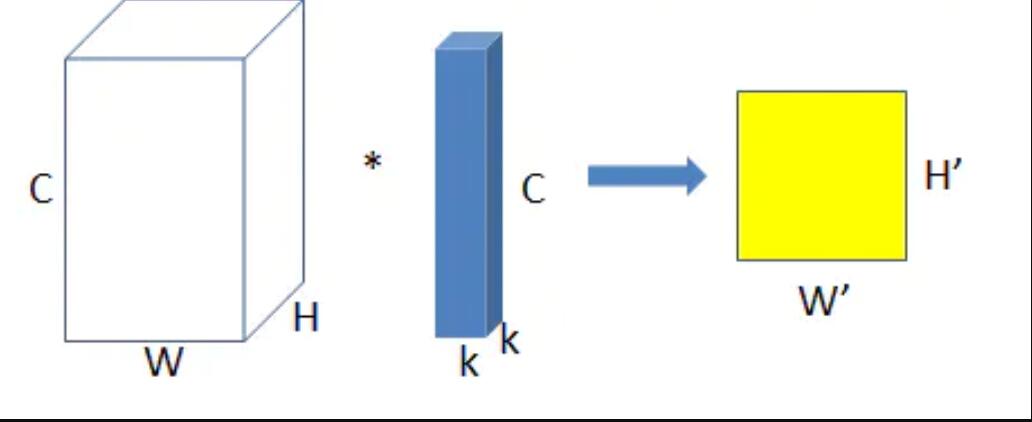
输入特征尺寸: W×H×C
卷积核尺寸: k×k×C
特征图尺寸: W’×H’
参数量params=k²C 注意这里是总的参数量
运算量=k²CC’W’H’,这里只考虑浮点乘数量,不考虑浮点加数量
- 分组卷积
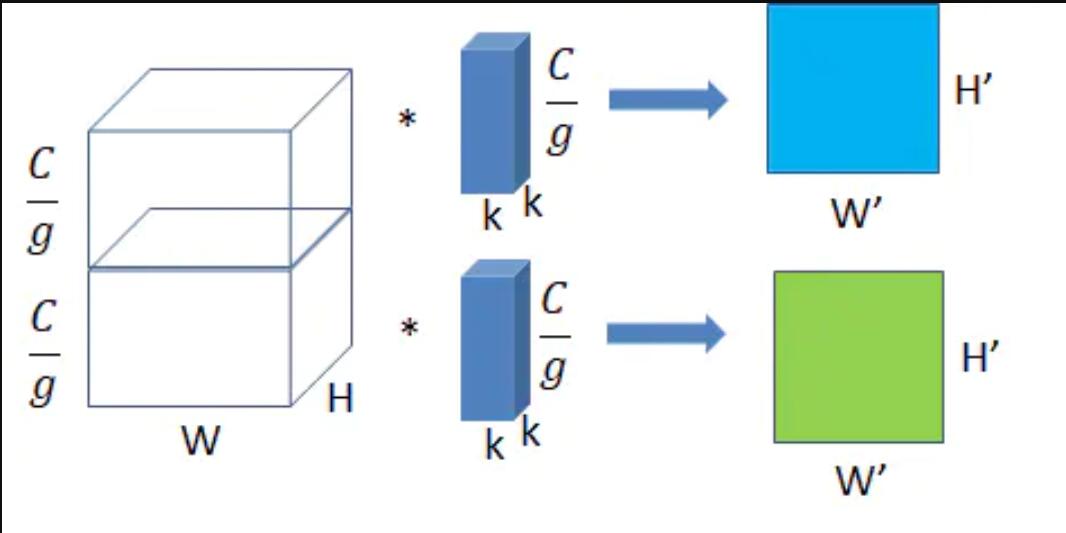
分组卷积将输入的特征分为g组,同样的,卷积核也被分为g组,让他们分组做卷积,最后得到g组特征图。
分组后输入特征尺寸(一组): W×H×(C/g)
分组后卷积核尺寸(一组): k×k×(C/g)
分组后特征图尺寸(一组): W’×H’
参数量params=k²×(C/g)×(C’/g)×g=(k²CC’)/g
运算量=k²(C/g)(C’/g)W’H’×g=(k²CW’H’)/g,这里只考虑浮点乘数量,不考虑浮点加数量
这样看来,我们用1/g的多的参数量和运算量得到了更多的特征!这就是它目前依旧存在,依旧坚挺的原因。它的优势在于减少了特征数量和运算量,那么效果如何呢?事实证明在某些情况下分组卷积的效果确实要比标准卷积要好,具体可以参照这里A Tutorial on Filter Groups (Grouped Convolution)
若要分析其原因,则是这种方法增加相邻层filter之间的对角相关性,而且能够减少训练参数,不容易过拟合。关于对角相关性,这篇博客里做出了解释,但是这只是实验结果,并没有明确说明是为什么。 传送门
接下来终于可以讲depthwise conv2d了,其实它非常简单。当分组卷积中的g=1时,就是普通的卷积;当分组卷积中的g=C也即组数等于特征通道数时,就是我们所说的depthwise conv2d。
例如下图,三通的的输入特征分为三组分别进行卷积,得到结果后再进行堆叠。